Tema 5: Momento Angular intrínseco

Figura 1. Sección transversal de una varilla de anchura infinitesimal con densidad lineal de carga \(\lambda\). En un tiempo dt la carga, con velocidad v en la dirección tangente a la varilla, recorre una distancia d\(\ell \) = v dt.

1Interacción entre dipolo y campo magnético

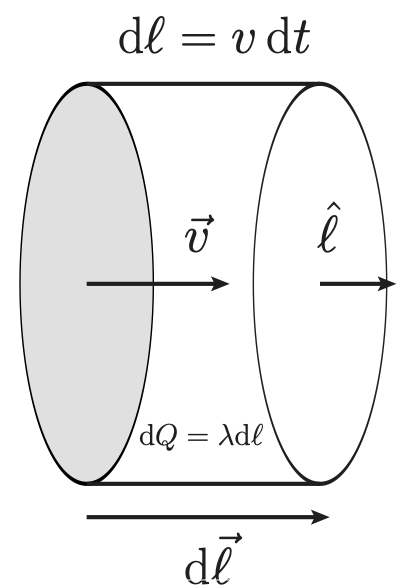
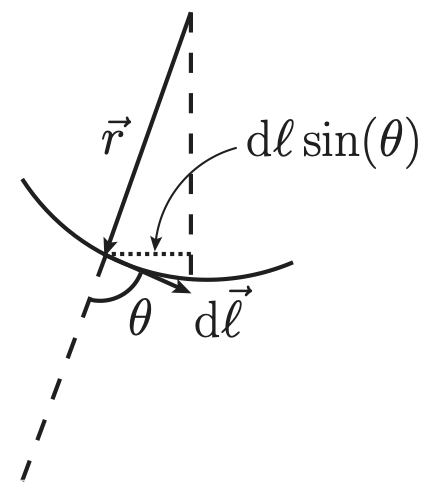
Los cuantos con momento dipolar no nulo reaccionan en presencia de un campo magnético externo. Consideremos un modelo simplificado, una espira circular, para describir el momento magnético dipolar de un electrón orbitando alrededor de un núcleo (esto permitirá una generalización para partículas con momento angular intrínseco). Como veremos en esta sección, el momento magnético de una espira plana sólo depende de su área así que presentamos aquí una demostración general. Empecemos recordando la fuerza que ejerce un campo magnético \(\vec{B}\) sobre una carga puntual \(q\) que se mueve con velocidad \(\vec{v}\) (esto es, la fuerza de Lorentz): \begin{equation} \vec{F} = q \,\vec{v} \times \vec{B} \,. \end{equation} Con este resultado podemos calcular la fuerza por unidad de longitud que ejerce el campo magnético sobre una varilla (no necesariamente contenida en un plano) por la que circula una corriente de intensidad \(I\). La fuerza sobre un diferencial de carga que se mueve en el seno del conductor es \begin{equation} {\rm d}\vec{F} = {\rm d} Q \,\vec{v} \times \vec{B} = (\lambda \vec{v} \times \vec{B}) {\rm d} \ell = \lambda v {\rm d} \vec{\ell} \times \vec{B}\,, \end{equation} donde en general la densidad y velocidad pueden depender de la posición (esto es, son campos escalares), y hemos usado \(\hat{\ell} {\rm d} \ell \equiv {\rm d} \vec{\ell}\). Veamos la carga \(\delta Q\) total atraviesa la superficie de la varilla \(S\) en el tiempo \(\delta t\), lo que sirve para calcular la intensidad de corriente, tal y como se ve en la figura 1 \begin{equation} \delta Q = \lambda v {\rm d} t, \longrightarrow I = \lambda v\,, \end{equation} que suponemos constante a lo largo de la varilla. Con este resultado obtenemos la fuerza por unidad de longitud sobre la varilla: \begin{equation} {\rm d} \vec{F} = I {\rm d} \vec{\ell} \times \vec{B}, \end{equation} con \({\rm d} \vec{\ell}\) tangente a la varilla en cada punto y en la dirección de la corriente. Como la espira es cerrada tenemos que \(\int {\rm d} \vec{\ell} = 0\) de modo que fuerza total sobre la espira es nula, con lo que su centro de masas no se acelera (y si estaba inicialmente en reposo, sigue igual). Supongamos ahora que la espira es plana y calculemos el momento de fuerza respecto de un punto contenido en el plano de la espira, suponiendo la intensidad de corriente en el sentido contrario a las agujas del reloj si \(I > 0\): \begin{equation} \vec{\tau} = \int \vec{r} \times {\rm d} \vec{F} = I \int \vec{r} \times ({\rm d} \vec{\ell} \times \vec{B}) \equiv - I \vec{B} \times \int \vec{r} \times {\rm d} \vec{\ell} - \int {\rm d} \vec{\ell} \times (\vec{B} \times \vec{r}), \end{equation} en donde en la segunda igualdad hemos usado la identidad de Jacobi para el doble producto vectorial¹. La primera integral es el doble del vector área \begin{equation} - I \vec{B} \times \int \vec{r} \times {\rm d} \vec{\ell} = 2 I \vec{S} \times \vec{B}\, . \label{eq:int1} \end{equation}

Figura 2. Vectores de posición y diferencial de varilla en la dirección de la corriente (sentido contrario a las agujas del rejol). La linea discontínua inferior es la prolongación del vector de posición, mientras que la superior tiene como longidud \(r \equiv | \vec{r} |\). La lína de puntos es la altura del triángulo, con longitud \(\sin (\theta) {\rm d} \ell\).

Para ver cómo emerge el área basta darse cuenta de que \(\vec r\) y \({\rm d}\vec\ell \) están siempre contenidos en el plano \(x,y\), con lo que su producto vectorial es en la dirección \(z\): \(\vec{r} \times {\rm d} \vec{\ell} = \sin (\theta) r {\rm d} \ell \hat{e}_k = 2 {\rm d} S \hat{e}_k = 2 {\rm d} \vec{S}\). El diferencial de superficie aparece porque \(\vec r\) y \({\rm d}\vec\ell \) son los lados de un triángulo de base \(r\) y altura \(\sin (\theta) {\rm d} \ell\). 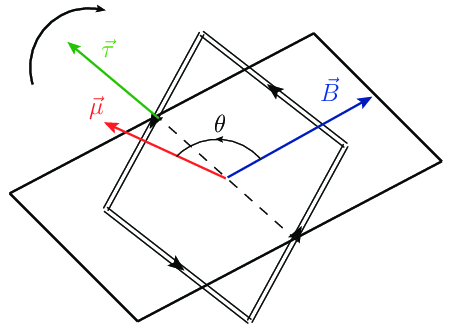Calculemos la segunda integral, para lo que usamos la identidad del doble producto vectorial:² \begin{equation} - \int {\rm d} \vec{\ell} \times (\vec{B} \times \vec{r}) = \int \vec{r} \left( {\rm d} \vec{\ell} \cdot \vec{B} \right) - \vec{B} \int {\rm d} \vec{\ell} \cdot \vec{r} \,. \end{equation} Usando el teorema de Stokes³ en la segunda integral y el hecho de que \(\vec{\nabla} \times \vec{r} \equiv \vec{0}\) vemos que este término se anula. Para el primero descomponemos \(\vec{r} = x \hat{e}_x + y \hat{e}_y\) y aplicamos Stokes como sigue \begin{equation} \int {\rm d} \vec{\ell} \cdot \Bigl( x \vec{B} \Bigr) = \int {\rm d} \vec{S} \cdot [\vec{\nabla} \times (x \vec{B})] = \int {\rm d} \vec{S} \cdot [(\vec{\nabla} x) \times \vec{B} ] = \vec{S} \cdot (\hat{e}_x \times \vec{B}) , \end{equation} en donde hemos usado la identidad \(\vec{\nabla}\!\times\!\bigl(a\,\vec{b}\,\bigr)= \bigl(\vec{\nabla}a\,\bigr)\!\times\! \vec{b} + a\bigl(\vec{\nabla}\!\times \!\vec{b}\,\bigr)\) y \(\vec{\nabla}x =\hat{e}_x\). Sumando la componente \(y \hat{e}_y\) y usando la propiedad cíclica del producto triple tenemos \begin{equation} \int \vec{r} \left( {\rm d} \vec{\ell} \cdot \vec{B} \right) = \hat{e}_x [\hat{e}_x \cdot (\vec{B} \times \vec{S})] + \hat{e}_y [\hat{e}_y \cdot (\vec{B} \times \vec{S})] = \vec{B} \times \vec{S}, \label{eq:int2} \end{equation} en donde hemos usado la descomposición de \(\vec{B} \times \vec{S}\) en componentes cartesianas y \(\hat{e}_z \cdot (\vec{B} \times \vec{S}) = 0\). Añadiendo los resultados de las ecuaciones (7) y (10) llegamos por fin a \begin{equation} \vec{\tau} = I \vec{S} \times \vec{B} \equiv \vec{\mu} \times \vec{B}, \end{equation} donde hemos definido el momento magnético de la espira \(\vec{\mu}\), proporcional al área y a la corriente, y normal a la primera con el sentido que marca la segunda según la regla de la mano derecha. El vector momento de fuerza estará contenido en el plano de la espira y por tanto la hará rotar respecto del eje que pasa por su centro de masas en la dirección de \(\vec{\tau}\).

Figura 3. Espira plana por la que circula una corriente \(I\) en el sentido contrario a las agujas del reloj, inmerso el seno de un campo magnético \(\vec{B}\). El momento magnético \(\vec{\mu}\) es normal a la superficie de la espira en dirección de la ley de la mano derecha. El campo magnético está contenido en el plano definido por sí mimo y el torque, y contiene al eje de giro. El momento de fuerza hace girar a la espira de modo que \(\vec{\tau}\) y \(\vec{\mu}\) tienden a alinearse.

Según este resultado, todo sistema que tenga un momento magnético no nulo tiende a orientarse en la dirección de un campo magnético en presencia de éste (sólo cuando \(\vec{B}\) y \(\vec{\mu}\) sean paralelos el momento de la fuerza será nulo). Veamos la energía asociada a una rotación producida por el par de fuerzas al girar el dipolo un ángulo definido entre \(\vec{B}\) y \(\vec{\mu}\) de manera que si éste aumenta los dos vectores se separan, movimiento en contra del par que implica un trabajo negativo, como se ve en la figura 3: \begin{equation} W = - \int_{\theta_1}^{\theta_2} {\rm d} \theta | \vec{\tau} | = - | \vec{\mu} | | \vec{B} | \int_{\theta_1}^{\theta_2} {\rm d} \theta \sin (\theta) = | \vec{\mu} | | \vec{B} | [\cos (\theta_2) - \cos (\theta_1)] = E_1 - E_2, \end{equation} de modo que la energía asociada es \(E = - \vec{\mu} \cdot \vec{B}\), siendo mínima cuando \(\vec{B}\) y \(\vec{\mu}\) son paralelos.

2Modelo Clásico: momento orbital del electrón

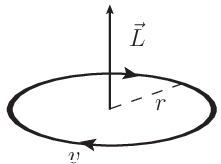
Consideremos por simplicidad un electrón orbitando en un átomo en una órbita circular de radio \(r\) y que se mueve con módulo de la velocidad constante \(v\) en el sentido contrario a las agujas del reloj, de modo que su momento angular es \(L = m_e v r\), apuntando en la dirección normal al plano orbital según la ley de la mano derecha. Dado que la corriente se define como el flujo de cargas positivas y el electrón está cargado negativamente, la dirección del momento magnético será la opuesta a la del momento angular orbital. El periodo del electrón (tiempo en dar una vuelta) es \(\tau = 2 \pi r / v\), con lo que, en valor absoluto la intensidad de corriente es \begin{equation} I = \frac{e}{\tau} = \frac{e v}{2 \pi r}, \end{equation} y usando que el área de la espira es \(\pi\,r^2\), su momento magnético toma la siguiente forma: \begin{equation} \vec{\mu} = - I \vec{S} = - \frac{e v r}{2} \hat{e}_z = - \frac{e \hbar}{2 m_e} \frac{\vec{L}}{\hbar} = - \mu_B \frac{\vec{L}}{\hbar} . \end{equation} En la segunda igualdad hemos definido el magnetón de Bohr \(\mu_B = e \hbar / (2 m_e) = 5.79 \times 10^{-11} \rm{MeV} / T\) del electrón. La energía que adquiere un electrón orbitando en presencia de un campo magnético que apunta en la dirección positiva del eje \(z\) es \(E = \mu_B B / \hbar\) y si consideramos ésta como un operador cuántico, sus autovalores respecto de una base de momento angular bien definido en el eje \(z~| \ell, m \rangle\) son \(E_m = m \mu_B B\), y por tanto no depende del momento angular total \(\ell\) (aunque la energía del Hamiltoniano total en general sí puede depender de este número cuántico). El desdoble de las lineas espectrales de un átomo en presencia de un campo magnético externo se conoce como efecto Zeeman. La física encerrada en estos autovalores es sencilla: si el Hamiltoniano tiene simetría esférica no podemos definir un eje \(z\) y por tanto las energías no pueden depender de \(m\) (aunque sí de \(\ell\) y por ejemplo del número cuántico principal). Si introducimos en el Hamiltoniano un vector constante (que no es un operador vectorial) éste señala una dirección privilegiada, con lo que rompemos la simetría esférica (\(\vec{B} \cdot \vec{L}\) no es un operador escalar) y las energías ya pueden depender de \(m\).

3Momento intrínseco del electrón

Figura 4. Momento angular de un electrón orbitando circularmente en el sentido de las agujas del reloj alrededor de un núcleo. También puede usarse como modelo del momento angular intrínseco o de espín, como un electrón rotando sobre sí mismo.

A raíz del experimento de Stern y Gerlach, Goudsmit y Uhlenbeck realizaron una segunda experiencia de efecto Zeeman en la que desdoble de las líneas espectrales observado se explicaba si los electrones tenían un momento angular intrínseco \(\vec{S}\) con número cuántico correspondiente al operador \(\vec{S}^2\) semientero \(S\) = 1/2, de modo la tercera componente toma valores \(S_z=\pm 1/2\).

La relación entre el momento angular intrínseco y el magnético está modificada por el factor giromagnético anómalo \(g_s\)^4/sup>. Añadiendo la contribución del momento angular orbital al momento magnético del electrón tenemos \begin{equation} \vec{\mu} = - \frac{\mu_B}{\hbar} (\vec{L} + g_s \vec{S}) . \end{equation} La ecuación de Dirac (relativista) con acoplamiento mínimo a campos electromagnéticos predice \(g_s=2\) para partículas puntuales. Correcciones cuánticas cambian este valor a \(g_s = 2.002331836\), en excelente acuerdo con medidas experimentales de precisión.

4Resonancia de espín

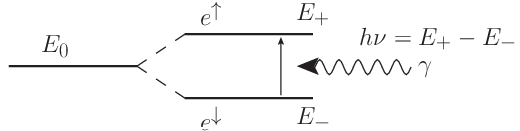
Figura 5. Resonancia producida por la absorción de un fotón con energía igual al desdoble entre niveles de energía.

Suponiendo que la energía asociada a la interacción con el campo magnético es pequeña comparada con la energía de ligadura del electrón al núcleo podemos usar teoría de perturbaciones a primer orden, con lo que la energía total es \(E = E_{\rm{lig}} + \mu_B B (m + g_s s_z) + \mathcal{O} (B^2)\), y en el caso de que el electrón esté en un orbital con \(m\) = 0 la modificación será solamente debida al espín, con lo que la energía de desdoble será \(\Delta E = E_+ - E_- = \pm \mu_B g_s B\). La energía del fotón producido en una transición entre estos dos niveles es \(E = h \nu = \mu_B g_s | B |\), y es la misma que debe tener un fotón incidente para inducir la transición, tal y como se muestra en la figura 5.

Si exponemos un material de estas características a un campo magnético externo y lo radiamos con un frente plano de fotones de la frecuencia adecuada, muchos de los fotones incidentes serán absorbidos. Tras un breve tiempo se emitirá un nuevo fotón, aunque no necesariamente en la dirección incidente, de modo que el electrón pueda absorber nuevos fotones incidentes. Este fenómeno se conoce como absorción resonante, y se manifiesta como una caída brusca en la intensidad de las ondas detectadas. En el laboratorio generamos el campo magnético mediante unas espiras y usamos la ley de Biot y Savart para calcular su valor en términos de la intensidad de corriente: \begin{equation} B = \mu_0 \left( \frac{4}{5} \right)^{3 / 2} \frac{n}{r} I, \end{equation} con \(\mu_0 = 4 \pi \times 10^{- 7} N / A^2\) la permeabilidad del vacío y \(n\) el número de espiras de la bobina. La intensidad de corriente que circula por estas espiras tiene una componente continua \(I_0\) (que podemos variar) superpuesta a una alterna (con intensidad \(I_1\) y frecuencia \(\omega\) fijas), tal que el campo magnético resultante tiene la siguiente forma:⁵ \begin{equation} B (t) = B_0 + B_1 \sin (\omega t) . \end{equation} La intensidad de la corriente continua \(I_0\) se puede medir en la práctica con un amperímetro, mientras que al amplitud del voltaje asociado a la corriente total puede ser visualizado en el canal X de un osciloscopio. La radiación incidente se genera con una fuente de radiofrecuencia que admite frecuencias entre \(\nu\) = 20 y 80 Hz (y que podemos medir), cuya amplitud se registra en el canal Y del mismo osciloscopio. La absorción resonante se observa como una serie de picos invertidos. Suponemos de entrada que \( B_0 \ge B_1\), así pues el campo magnético siempre apunta en la misma dirección y sentido: \(|B| = B\).

Figura 6. Valor de la diferencia de energía entre los niveles desdoblados de un electrón sometido a un campo magnético con una componente constante y una sinusoidal, con el tiempo y la energía medidos en unidades arbitrarias. Las lineas horizontales se corresponden con la energía de los fotones de radiofrecuencia. En la parte superior izquierda se muestra la condición de absorción en los máximos (rojo), mínimos (verde) y el centro (azul), obtenida para tres valores de \(B_0\), que desplaza verticalmente la sinusoide. En el resto de figuras se muestra para qué valores de \(t\) en un mismo periodo tiene lugar la resonancia en distintas situaciones: arriba a la derecha para \(B_0 > B_1\), abajo izquierda para \(0 < B_0 < B_1\) y abajo a la derecha si \(B_0=0\). Según el valor de la energía del fotón puede haber de una a cuatro soluciones por periodo.

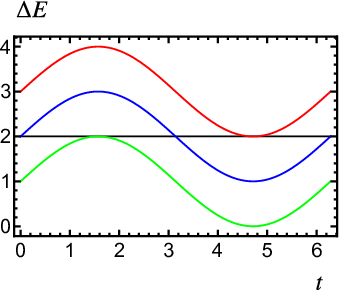
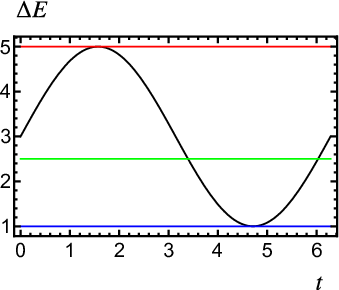
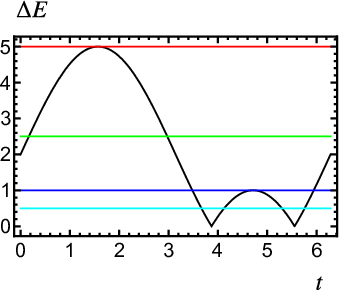
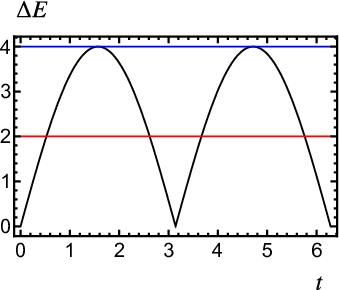
Para una frecuencia determinada podemos ajustar el valor de \(B_0\) de modo que se produzca absorción resonante. Habrá absorción si se cumple \(g_s \mu_B (B_0 - B_1) \leq h \nu \leq g_s \mu_B (B_0 + B_1)\) y en general tendrá lugar para dos valores de \(t\) por ciclo (ver figura 6 ). En la práctica, para una frecuencia dada se ajusta el valor de \(B_0\) (modificando la corriente \(I_0\) ) para que se produzca absorción en los valores extremos de la desigualdad \(h \nu = g_s \mu_B (B^{\pm}_0 \pm B_1) \equiv g_s \mu_B B^{\pm}\) (una absorción por periodo) así como en el centro \(h \nu = g_s \mu_B B^{\rm{cent}}_0\) (dos absorciones por periodo), correspondientes al máximo, mínimo y el centro de la componente sinusoidal de \(B\) . Estos valores para los se produce resonancia están ordenados \(B_0^+ < B_0^- < B_0^{\min}\) y cumplen \(B_0^+ + B_0^-=2 B^{\rm{cent}}_0\). Para frecuencias tales que \(h \nu < 2 g_s \mu_B B_1\) no se puede encontrar ningún valor de \(B_0\) para el que tenga lugar resonancia en el máximo (esto es, no se puede encontrar \(B^+\)), ya que \(B^{\max} \geqslant 2 B_1\) (el valor mínimo se obtiene para \(B_0=B_1\) bajo la hipótesis \(B_0 \geqslant B_1\)). Sin embargo, sí existe absorción en el mínimo, puesto que \(B^-=B_0 - B_1> 0\) (por hipótesis), y en centro, que cumple \(B^{\rm{cent}} = B_0 > 0\) (siempre). Si permitimos \(B_0 < B_1\),⁶ no se puede encontrar un valor de \(B_0\) para tener absorción en el máximo si \(h \nu < g_s \mu_B B_1\), ya que en este caso \(B^+ \geqslant B_1\) (valor mínimo para \(B_0=0\)⁷), aunque sí se pueden encontrar condiciones resonantes en el centro (\(| B^{\rm{cent}} | = B_0 > 0\)) y el mínimo (\(| B^- | = | B_0 - B_1 | > 0\)).

Figura 7. Resonancia de espín (señal en rojo) detectada por un osciloscopio cuando un electrón es sometido a radiación electromagnética en el seno de un campo magnético oscilante (señal en azul). En la izquierda, centro y derecha se muestra la pantalla del osciloscopio cuando la absorción resonante se produce en el máximo, centro y mínimo del campo magnético, respectivamente. Para que las medidas sean más precisas es conveniente ajustar el offset de la radiación de modo que el mínimo coincida con los puntos extremos y central de la señal del campo magnético.

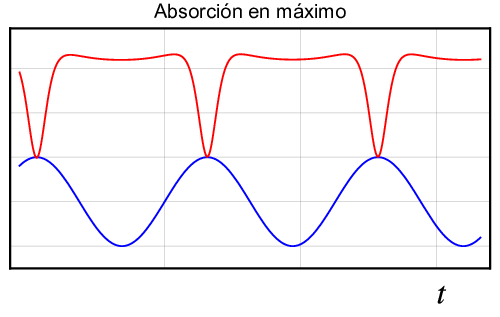
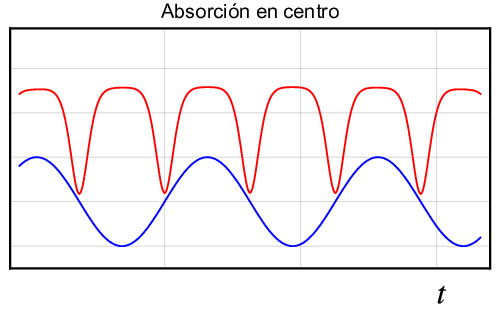
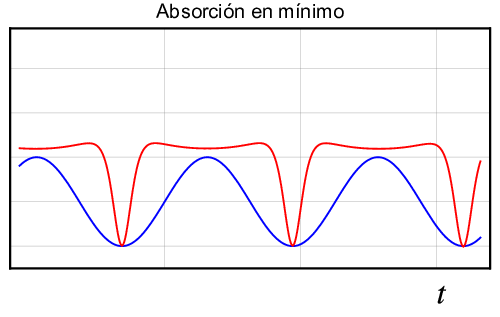
Las medidas de \(B^+_0, B^{\rm{cent}}_0\) y \(B^-_0\) se hacen registrando las señales de la corriente eléctrica que pasa por unas espiras en el canal de un osciloscopio, y la intensidad de las ondas electromagnéticos en el otro canal del mismo, tal y como se muestra en la figura 7 en colores azul y rojo, respectivamente. Cuando se produce absorción se observan una serie de picos invertidos, como se ve la figura, y dada una frecuencia tenemos que ajustar \(B_0\) para obtener resonancia en los máximos, centro y mínimos, tal y como se observa en los gráficos de la izquierda, centro y derecha, respectivamente.

Generamos de este modo tétradas de datos (una por valor de la frecuencia) \(\{ \nu, B^+_0, B^{\rm{cent}}_0, B^-_0 \}\) (tríadas en el caso \(h \nu < g_s \mu_B B_1\)) que se corresponden con tres rectas: \begin{equation} h \nu=\left\{ \begin{array}{l} \mu_B g_s (B^+_0 + B_1)\\ \mu_B g_s B^{\rm{cent}}_0\\ \mu_B g_s (B^-_0 - B_1) \end{array} \right., \end{equation} que podemos ajustar individualmente por mínimos cuadrados para obtener tres predicciones para \(g_s\). En dos de las rectas obtenemos también el valor de \(B_1\), que se puede comparar entre ellas y con una medida directa hecha con el multímetro. También se pueden combinar todos los datos en un solo ajuste global, consiguiendo así una mayor significancia estadística. Para cada tétrada de datos generamos tres puntos \(\{ x, y \}\) con valores \(\{ \nu, B^-_0 \}\), \(\{ 2 \nu, B_0^{\rm{cent}} + B_0^- \}\) y \(\{ 3 \nu, B_0^+ + 2 B_0^- \}\),⁸ y que obedecen la misma ecuación lineal \(h y = g_s \mu_B (x - B_1)\), por lo que están alineados y de un solo ajuste obtenemos \(g_s\) y \(B_1\) .

Terminamos la presentación de la resonancia del espín discutiendo cuántas absorciones tienen lugar en un periodo (pueden ser entre 1 y 4) según los valores de \(\nu\), \(B_0\) y \(B_1\). Si \(B_0>B_1\) tenemos una solución (en el máximo y mínimo, respectivamente) si \(h \nu = g_s \mu_B (B_0 \pm B_1)\) y dos soluciones si \(h\nu\) está entre esos dos valores. Si \(0 < B_0 < B_1\) tenemos una solución si \(h \nu=g_s \mu_B (B_0 + B_1)\) [en el máximo], dos soluciones si \(g_s \mu_B (B_1 - B_0) < h \nu < g_s \mu_B (B_0 + B_1)\) [entre el máximo absoluto y el relativo], tres soluciones si \(h \nu=2 g_s \mu_B (B_1 - B_0)\) [en el máximo relativo] y cuatro si \(h \nu < g_s \mu_B (B_1 - B_1)\) [por debajo de éste]. Finalmente, si \(B_0=0 \) tenemos dos soluciones si \(h \nu=g_s \mu_B B_1\) (en el máximo) y cuatro si \(h \nu < g_s \mu_B B_1\) (por debajo del mismo).

---

1. Esto es \(\vec{A} \times (\vec{B} \times \vec{C}) + \vec{C} \times (\vec{A} \times \vec{B}) + \vec{B} \times (\vec{C} \times \vec{A}) = 0\).↩︎

2. A saber \((\vec{A} \times \vec{B}) \times \vec{C} = (\vec{A} \cdot\vec{C}) \vec{B} - (\vec{B} \cdot\vec{C}) \vec{A}\), que puede ser obtenida contrayendo dos símbolos de Levi-Cività y usando \(\varepsilon_{ijk} \varepsilon_{imn} = \delta_{j m} \delta_{k n} - \delta_{j n} \delta_{k m}\).↩︎

3. A saber: \(\int_{\partial S} {\rm d} \vec{\ell} \cdot \vec{F} = \int_S \! \! {\rm d} \vec{S} \cdot (\vec{\nabla} \times \vec{F})\). También podríamos usar el teorema de Green.↩︎

4. Para nucleones tenemos \(\vec{\mu} = - g_N \mu_N \vec{S} / \hbar\) con \(\mu_N = e \hbar / (2 m_N)\) el magnetón nuclear y \(g_N\) los factores giromagnéticos anómalos que reflejan la subestructura de protón y neutrón en términos de quarks: \(g_p = 2.798\) y \(g_n = - 1.913\).↩︎

5. La frecuencia de la corriente alterna no debe confundirse con la de los fotones de radiofrecuencia.↩︎

6. En el caso de que \(0 < B_0 < B_1\) la estructura en máximos y mínimos de \(| B |\) se altera (aunque no la de \(B\)), ya que aparece un segundo máximo local (correspondiente al mínimo de \(B\)) con valor \(B_1 - B_0 > 0\) (para un valor del campo \(B = B_0 - B_1 < 0\)) y  dos mínimos por periodo con valor \(0\). Si tenemos \(B_0 = 0\) entonces sólo hay máximos absolutos (dos por periodo) con altura \(B_1\) (correspondientes a \(B = \pm B_1\)) y mínimos absolutos con altura nula (también dos por periodo). Ver figura 6 para aclaración gráfica.↩︎

7. No tiene sentido considerar valores negativos de \(B_0\), ya que es equivalente a tener \(B_0\) positivo y el campo apuntando en dirección contraria.↩︎

8. Se podrían considerar las combinaciones \(\{ \nu, B^+_0 \}\), \(\{ 2 \nu, B_0^{\rm{cent}} + B_0^+ \}\) y \(\{ 3 \nu, B_0^- + 2 B_0^+ \}\), pero en este caso no podríamos usar aquellos valores de \(\nu\) para los que \(B_0^+\) no está definido. Con la combinación propuesta, estos valores todavía proporcionan 2 puntos, manteniéndose el mismo número de datos que en el caso de ajustar tres rectas.↩︎

Soluciones a la condición de resonancia

Mueve los sliders para cambiar los valores de \(B_0\), \(B_1\) y \(\Delta E\) para ver en qué valores de t se produce resonancia de espín en un ciclo de la corriente alterna. Las unidades de energía, campo magnético y tiempo son arbitrarias, pero el campo magnético está multiplicado por \(g_s\mu_B\) de modo que en el la dirección vertical del gráfico aparecen magnitudes con unidades de energía.